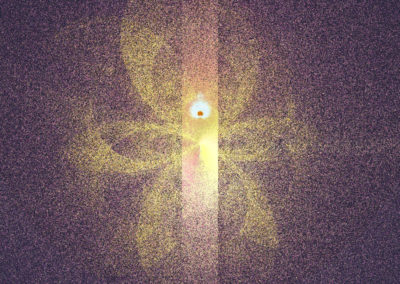
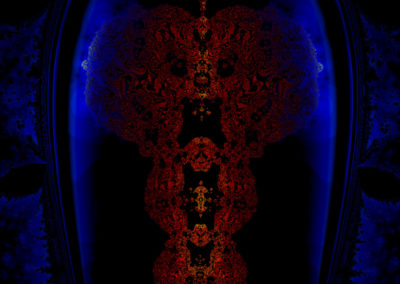
Fractal 026 C – Nativity
Part of BEYOND series – 09 2021
cell . microbe . nativity . night . purple . space
Fractal 026 C – zoom level 1
Fractal 026 C – zoom level 2
Data
This digital works is created exclusively from fractals, with 0% AI generated. It can therefore be converted into a set of functions and parameters that can be the basis for the training of an AI.
The mathematical formulas and parameter combinations corresponding to each fractal are presented below. In each case, the numerical characters have been replaced by â– to prevent unauthorized reproduction. If you are interested in using the full data set to train an AI, please contact Philippe.
Fractal 026 C - Nativity - Part of BEYOND series - 09.2021
Fractal_â– â– â– _C {
fractal:
title="Fractal_â– â– â– _C" width=â– â– â– â– height=â– â– â– â– layers=â–
credits="Philoxerax;â– /â– /â– â– â– â– " antialiasing=yes
layer:
caption="Background" opacity=â– â– mergemode=subtraction
mapping:
center=-â– .â– â– â– â– â– â– â– â– â– â– â– â– â– â– â– /â– .â– â– â– â– â– â– â– â– â– â– â– â– â– â– â– magn=â– â– â– â– .â– â– â– â–
angle=-â– â– .â– â– â– â–
formula:
maxiter=â– â– â– filename="Standard.ufm" entry="Mandelbrot" p_start=â– /â–
p_power=â– /â– p_bailout=â– â– â–
inside:
transfer=none offset=â– â– â– repeat=no solid=â– â– â– â– â– â– â– â– â– â–
outside:
transfer=cube solid=â– â– â– â– â– â– â– â– â– â– filename="Standard.ucl"
entry="Smooth" p_power=â– /â– p_bailout=â– â– â– .â–
gradient:
smooth=yes rotation=â– â– index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â–
color=â– â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– â–
index=â– â– color=â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– â–
index=â– â– color=â– â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– â– index=â– â–
color=â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– â–
index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– index=â– â– â–
color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â–
index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â– â–
color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– â–
index=â– â– â– color=â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â– â–
color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– index=â– â– â–
color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â–
opacity:
smooth=no index=â– opacity=â– â– â–
layer:
caption="Background" opacity=â– â– â– mergemode=softlight
mapping:
center=-â– .â– â– â– â– â– â– â– â– â– â– â– â– /-â– .â– â– â– â– â– â– â– â– â– â– â– â– â– magn=â– â– â– .â– â– â– â– â– angle=â– .â– â– â– â–
formula:
maxiter=â– â– â– â– percheck=off filename="dmj.ufm" entry="dmj-HNovaMandel"
p_start=â– /â– p_power=â– /â– p_bailout=â– .â– â– â– â– â– p_relax=â– /â–
inside:
transfer=none solid=â– â– â– â– â– â– â– â– â– â–
outside:
transfer=linear
gradient:
smooth=yes index=â– color=â– index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â– â–
color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– â–
opacity:
smooth=no index=â– opacity=â– â– â–
layer:
caption="Background" opacity=â– â– â– mergemode=hardlight
mapping:
center=â– .â– â– â– â– â– â– â– â– â– â– /â– .â– â– â– â– â– â– â– â– â– â– â– magn=â– â– .â– â– â– â– â– â– angle=-â– â– .â– â– â– â–
formula:
maxiter=â– â– â– â– percheck=off filename="dmj.ufm" entry="dmj-ManyNova"
p_power=â– /â– p_bailout=â– .â– â– â– â– â– p_relax=â– /â– p_scale=â– .â– p_jscale=â– .â–
inside:
transfer=none
outside:
transfer=linear
gradient:
smooth=yes rotation=-â– index=â– â– color=â– â– â– â– â– â– â– â– index=â– â–
color=â– â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â–
index=â– â– color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â– â–
color=â– â– â– â– â– â– â– â– index=-â– â– color=â–
opacity:
smooth=no index=â– opacity=â– â– â–
layer:
caption="Layer â– " opacity=â– â– mergemode=multiply
mapping:
center=-â– .â– â– â– â– â– â– â– â– â– â– â– â– /â– .â– â– â– â– â– â– â– â– â– â– â– â– magn=â– â– .â– â– â– â–
formula:
maxiter=â– â– â– filename="anon.ufm" entry="TZâ– â– â– â– -â– â– "
inside:
transfer=none
outside:
transfer=linear
gradient:
smooth=yes rotation=-â– â– â– index=â– color=â– â– â– â– â– index=â– â– â– color=â– â– â–
index=-â– â– â– color=â– â– â– â– â– â– â– index=-â– â– â– color=â– â– â– index=-â– â– â–
color=â– â– â– â– â– â– â– index=-â– â– â– color=â– â– â– â– â– â– â– index=-â– â– â– color=â– â– â– â– â– â– â– â–
index=-â– â– â– color=â– â– â– â– â– â– â– â– index=-â– â– â– color=â– â– â– â– â– â– â– â– index=-â– â– â–
color=â–
opacity:
smooth=no index=â– opacity=â– â– â–
layer:
caption="Layer â– " opacity=â– â– mergemode=lighten
mapping:
center=-â– .â– â– â– â– â– â– â– â– â– â– â– â– â– /â– .â– â– â– â– â– â– â– â– â– â– â– â– â– magn=â– â– .â– â– â– â– â– â–
formula:
maxiter=â– â– â– filename="anon.ufm" entry="TZâ– â– â– â– -â– â– "
inside:
transfer=none
outside:
transfer=linear
gradient:
smooth=yes rotation=-â– â– â– index=â– color=â– â– â– â– â– index=â– â– â– color=â– â– â–
index=-â– â– â– color=â– â– â– â– â– â– â– index=-â– â– â– color=â– â– â– index=-â– â– â–
color=â– â– â– â– â– â– â– index=-â– â– â– color=â– â– â– â– â– â– â– index=-â– â– â– color=â– â– â– â– â– â– â– â–
index=-â– â– â– color=â– â– â– â– â– â– â– â– index=-â– â– â– color=â– â– â– â– â– â– â– â– index=-â– â– â–
color=â–
opacity:
smooth=no index=â– opacity=â– â– â–
layer:
caption="Layer â– " opacity=â– â– â– mergemode=lighten
mapping:
center=-â– .â– â– â– â– â– â– â– â– â– â– â– â– â– /â– .â– â– â– â– â– â– â– â– â– â– â– â– â– magn=â– â– .â– â– â– â– â– â–
formula:
maxiter=â– â– â– filename="anon.ufm" entry="TZâ– â– â– â– -â– â– "
inside:
transfer=none
outside:
transfer=linear
gradient:
smooth=yes index=â– color=â– â– â– â– â– â– â– index=â– â– color=â– â– â– index=â– â–
color=â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– â–
index=â– â– color=â– â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– â– index=â– â– color=â–
index=â– â– â– color=â– â– â– â– â– index=â– â– â– color=â– â– â–
opacity:
smooth=no index=â– opacity=â– â– â–
layer:
caption="Background" opacity=â– â– â– mergemode=overlay
mapping:
center=-â– .â– â– â– â– â– â– â– â– â– â– â– â– /â– .â– â– â– â– â– â– â– â– â– â– â– â– â– magn=â– â– .â– â– â– â– â– â–
formula:
maxiter=â– â– â– filename="anon.ufm" entry="TZâ– â– â– â– -â– â– "
inside:
transfer=none
outside:
transfer=linear
gradient:
smooth=yes index=â– color=â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â– â– â– â– index=â– â– â–
color=â– â– â– â– â– index=â– â– â– color=â– â– â–
opacity:
smooth=no index=â– opacity=â– â– â–
layer:
caption="Layer â– " opacity=â– â–
mapping:
center=-â– .â– â– â– â– â– â– â– â– â– â– â– /â– .â– â– â– â– â– â– â– â– â– â– â– â– magn=â– â– .â– â– â– â– â– â– angle=â– â– â– .â– â– â– â–
formula:
maxiter=â– â– â– filename="anon.ufm" entry="TZâ– â– â– â– -â– â– "
inside:
transfer=none
outside:
transfer=linear
gradient:
smooth=yes index=â– color=â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– â– index=â– â–
color=â– â– â– â– â– â– â– â– index=â– â– color=â– â– â– â– â– â– â– â– index=â– â– â– color=â– â– â– â– â–
index=â– â– â– color=â– â– â–
opacity:
smooth=no index=â– opacity=â– â– â–
}
Mandelbrot {
;
; Generic Mandelbrot set.
;
init:
z = @start
loop:
z = z^@power + #pixel
bailout:
|z| <= @bailout
$IFDEF VERâ– â–
perturbinit:
#dz = â–
perturbloop:
if @power == (â– , â– )
#dz = â– â– #z â– #dz + sqr(#dz) + #dpixel
elseif @power == (â– , â– )
complex zâ– = sqr(#z)
complex dzâ– = sqr(#dz)
#dz = â– â– zâ– â– #dz + â– â– #z â– dzâ– + #dz â– dzâ– + #dpixel
else ; power â–
complex zâ– = sqr(#z)
complex dzâ– = sqr(#dz)
complex zdzâ– = â– â– #zâ– #dz
#dz = #dpixel + zdzâ– â– zâ– + â– â– zâ– â– dzâ– + zdzâ– â– dzâ– + sqr(dzâ– )
endif
$ENDIF
default:
title = "Mandelbrot"
center = (-â– .â– , â– )
helpfile = "Ufâ– .chm"
helptopic = "Html\formulas\standard\mandelbrot.html"
$IFDEF VERâ– â–
rating = recommended
$ENDIF
$IFDEF VERâ– â–
perturb = @power == (â– , â– ) || @power == (â– , â– ) || @power == (â– , â– )
$ENDIF
param start
caption = "Starting point"
default = (â– ,â– )
hint = "The starting point parameter can be used to distort the Mandelbrot \
set. Use (â– , â– ) for the standard Mandelbrot set."
endparam
param power
caption = "Power"
default = (â– ,â– )
hint = "This parameter sets the exponent for the Mandelbrot formula. \
Increasing the real part to â– , â– , and so on, will add discs to \
the Mandelbrot figure. Non-integer real values and non-zero \
imaginary values will create distorted Mandelbrot sets. Use (â– , â– ) \
for the standard Mandelbrot set."
endparam
float param bailout
caption = "Bailout value"
default = â– .â–
min = â– .â–
$IFDEF VERâ– â–
exponential = true
$ENDIF
hint = "This parameter defines how soon an orbit bails out while \
iterating. Larger values give smoother outlines; values around â– \
give more interesting shapes around the set. Values less than â– \
will distort the fractal."
endparam
switch:
type = "Julia"
seed = #pixel
power = power
bailout = bailout
}
dmj-HNovaMandel {
;
; This is the Halley Nova fractal (Mandelbrot
; form), a modified Halley-style fractal. This
; is an adaptation of Paul Derbyshire's Halley
; Nova formulas for FractInt, which are based
; on his "Nova" formulas derived from classical
; Newton's Method fractals.
;
init:
complex nsquaredplusn = sqr(@power) + @power
complex nsquaredminusn = sqr(@power) - @power
complex zton = (â– ,â– )
complex zold = (â– ,â– )
z = @start
loop:
zold = z
zton = z^@power
z = z - (â– â– @powerâ– z â– (zton-â– )) â– @relax / \
(nsquaredplusnâ– zton + nsquaredminusn) + #pixel
bailout:
|z - zold| > @bailout
default:
title = "HalleyNova (Mandelbrot)"
helpfile = "dmj-pub\dmj-pub-uf-hn.htm"
maxiter = â– â– â– â–
periodicity = â–
center = (-â– .â– ,â– )
magn = â– .â–
param start
caption = "Start Value"
default = (â– ,â– )
hint = "Starting value for each point. You can use this to \
'perturb' the fractal."
endparam
param power
caption = "Exponent"
default = (â– ,â– )
hint = "Overall exponent for the equation. (â– ,â– ) gives \
the classic HalleyNovaM type."
endparam
param bailout
caption = "Bailout"
default = â– .â– â– â– â– â–
hint = "Bailout value; smaller values will cause more \
iterations to be done for each point."
endparam
param relax
caption = "Relaxation"
default = (â– ,â– )
hint = "This can be used to slow down the convergence of \
the formula."
endparam
switch:
type = "dmj-HNovaJulia"
seed = #pixel
power = @power
bailout = @bailout
relax = @relax
}
dmj-ManyNova {
;
; This formula breaks the image up into a grid of
; squares, each square containing a small Nova Julia set
; using the c value from the center of the square.
;
init:
float iscale = â– / @scale
c = round(#pixel â– @scale) â– iscale
z = (#pixel - c) â– @scale â– @jscale
complex zsquared = (â– ,â– )
complex zcubed = (â– ,â– )
complex zold = (â– ,â– )
loop:
IF (@power == (â– ,â– )); special optimized routine for power â–
zsquared = sqr(z)
zcubed = zsquared â– z
zold = z
z = z - @relax â– (zcubed-â– ) / (â– â– zsquared) + c
ELSE
zold = z
z = z - @relax â– (z^@power-â– ) / (@power â– z^(@power-â– )) + c
ENDIF
bailout:
|z-zold| > @bailout
default:
title = "ManyNova"
helpfile = "dmj-pub\dmj-pub-uf-manynova.htm"
maxiter = â– â– â– â–
periodicity = â–
center = (â– ,â– )
magn = â– .â–
param power
caption = "Exponent"
default = (â– ,â– )
hint = "Overall exponent for the equation. (â– ,â– ) gives \
the classic NovaM type."
endparam
param bailout
caption = "Bailout"
default = â– .â– â– â– â– â–
hint = "Bailout value; smaller values will cause more \
iterations to be done for each point."
endparam
param relax
caption = "Relaxation"
default = (â– ,â– )
hint = "This can be used to slow down the convergence of \
the formula."
endparam
param scale
caption = "Julia Density"
default = â– .â–
hint = "Specifies the density of separate Julia sets; higher \
numbers will produce more divisions."
endparam
param jscale
caption = "Julia Zoom"
default = â– .â–
hint = "Specifies the zoom level of Julia sets within each division."
endparam
}
TZâ– â– â– â– -â– â– {
;
;from TieraZonâ– fl-â– â– -â– â– .fll
;â– â– .) init z = â– ; z = z-(zâ– zâ– -tâ– zcos-z)/(â– â– zâ– -zsin-z)+c;
;
init:
z = â–
t = z
loop:
z = z - (z â– z^â– - t â– cos(z) - z) / (â– â– z^â– - sin(z) - z) + #pixel
bailout:
|z| < â–
}
